因果推断与科学评估
Date:
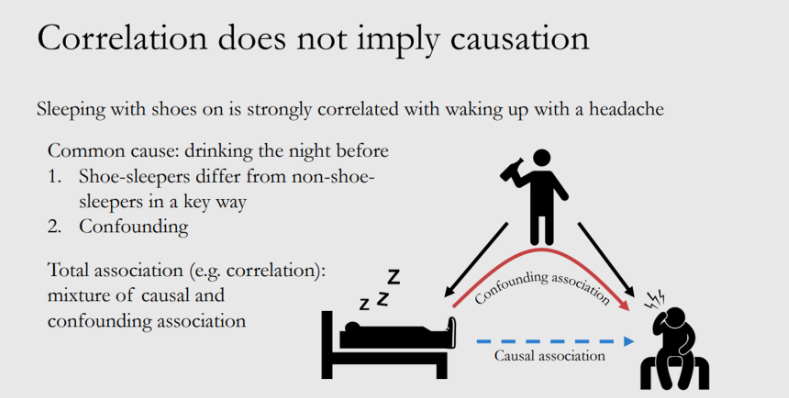
实践经验发现,穿鞋睡觉的人第二天起床大概率都会头疼,我们可以确定“穿鞋睡觉”和“起床头疼”有正相关性。 那么,“睡觉穿鞋”是否是“起床头疼” 的原因? 相关性是否可以直接等价于因果性?什么情况下相关性=因果性? 因果性如何度量评估?
为什么要做因果推断
实践经验发现,穿鞋睡觉的人第二天起床大概率都会头疼,我们可以确定“穿鞋睡觉”和“起床头疼”有正相关性。 那么,“睡觉穿鞋”是否是“起床头疼” 的原因? 相关性是否可以直接等价于因果性?什么情况下相关性=因果性? 因果性如何度量评估?
因果推断两大理论框架
因果推断应用最广泛的两大理论框架为结构因果模型(Structural Causal Model,简称SCM)和潜在结果框架(Potential Outcome Framework),这两者的研究视角不同,但本质是等价的, Judea Pearl 在他的著作《Causality: models, reasoning, and inference》中介绍了这两种框架的等价性。
 潜在结果框架( Potential Outcome Framework )关注在因果效应评估,更适用于工业界的场景和问题,下文主要从潜在结果框(鲁宾因果框架)架去阐述,同时结合因果图给出白盒解释。
潜在结果框架( Potential Outcome Framework )关注在因果效应评估,更适用于工业界的场景和问题,下文主要从潜在结果框(鲁宾因果框架)架去阐述,同时结合因果图给出白盒解释。
基本概念
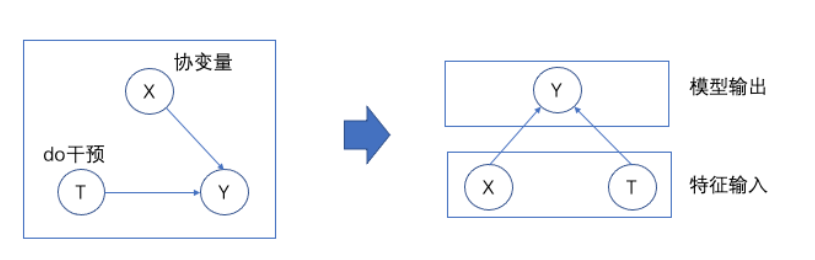
因果图:在有向图中,每个节点都是其子节点的直接原因。X 是 Y 的父节点,X 就是 Y 的直接原因
do算子(或者d算子):干预动作的意思 ,因果中常常讲的treatment组=干预组=实验组,与之对应的control组=未干预组=对照组。
协变量: 也可以称为混杂变量,是影响实验变化和结果的潜在因素,广义上普遍认为就是算法所说的特征。
观测结果observe outcome,是真实的存在的,如实验组做了干预之后的结果是什么。
潜在结果potential outcome,是不存在的真实,如实验组虽然做了干预,但是如果没做干预的结果是什么,这也是论文中常提到的反事实
RCT(Randomized Controlled Trial):随机对照试验,随机对照试验的核心特征是随机分配;参与者被随机分为两组或多组,其中一组接受干预措施,另一组作为对照组,通常接受安慰剂或标准治疗;随机分配可以消除偏见,确保各组在开始时是相似的。
Uplift原理-因果效应
Uplift Model预测的是某种干预对个体状态或行为的因果效应,即ITE(individual treament effect),对同一对象干预和不干预的效果差值。用公式可表示为:
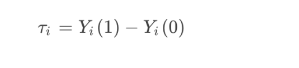
但是,显然无法同时获得一个用户在干预和未干预条件下的转化情况,因此我们可以通过ATE(average treatment effect)获得,即所有对象都接受干预和不干预的平均效果差值,公式表示为:
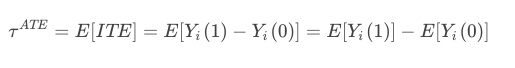
这里关注的是大数下的平均结果,“所有对象”可以通过随机对照试验RCT来获得,即干预组和对照组的人群同质。
但我们日常应用中并不关心所有对象,我们只关心我们对应场景或者某个特定人群群体的因果效应,也是通过RCT数据来确保X条件下人群同质,即CATE(Conditional average treatment effect):
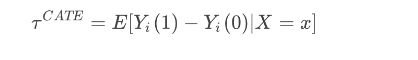
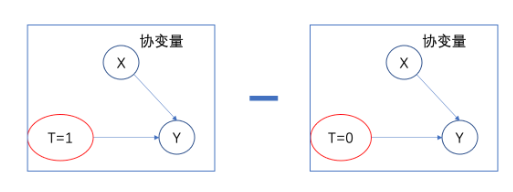
基本假设条件是无混杂性Unconfoundeness,无混杂性条件下 Correlation does imply Causation ,即相关性=因果性
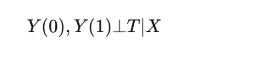
RCT实验核心是为了获取RCT数据,RCT数据具有哪些特质来保证无混杂性Unconfoundedness?无混杂条件下,如何推导出来相关性=因果性?
我们先从ATE
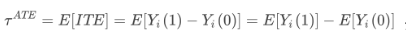
开始聊,即对所有对象而言,RCT数据如何确保因果性的成立的。
RCT数据
RCT数据特性:
Comparability and covariate balance:可比且协变量均衡 Exchangeability:干预组和对照组可交换 No backdoor paths:不存在后门路径
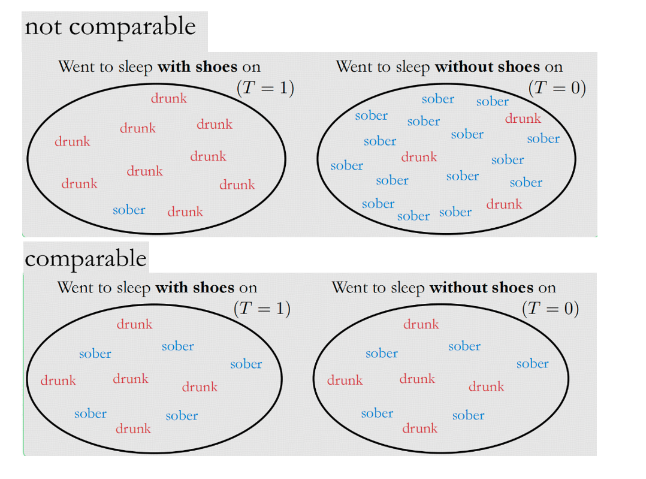
Comparability and covariate balance
协变量X的分布在任何 Treatment,control组下都是一致的
| <=> P(X | T=1) 和 P(X | T=0) 是同分布的 |
| <=> 在 t=1 时,P(X | T=1)=P(X);t=0 时,P(X | T=0)=P(X),无论 t 等于任何值的情况下,分布都是一样的。 |
示例:在“睡觉穿鞋”是否导致“起床头疼”这个案例中,我们设定干预组T=”睡觉穿鞋“,对照组T=”睡觉不穿鞋“, 此时我们要求两个组中X=”喝酒的人“的占比一致,比如都为50%。
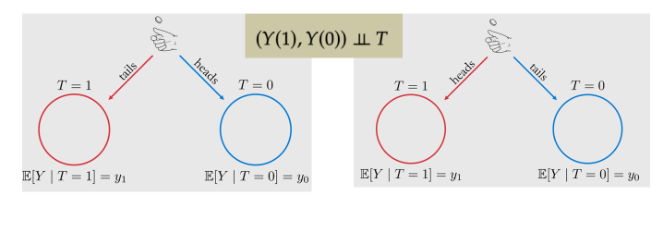
Exchangeability
即:t (treatment)和 y 的潜在结果( potential outcome )是独立不相关
将treatment组和control组人群进行替换,结果不变,T对于实验组和对照组的作用一致无差别
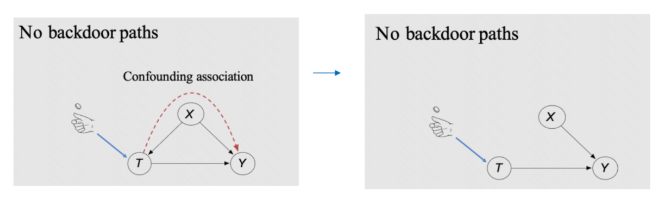
No backdoor paths
在T和 Y之间以 “T 为开始“,指向Y的箭头为结尾的路径,定义为前门路径
在T和 Y之间以”指向 T 的箭头为开始“同时指向Y的路径,定义为后门路径
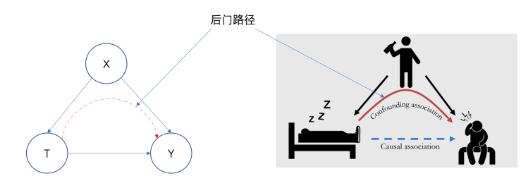
示例: 喝酒导致人睡觉不穿鞋,喝酒也能够带来头痛。 但是,整体设计干预组T=”睡觉穿鞋“以及对照组T=”睡觉不穿鞋“时,忽视喝酒的因素,进而得到穿鞋睡觉导致头痛的结论。
无后们路径,即所有影响结果的协变量都被完整观测且确保covariate balance,不存在任何其他对结果有影响的协变量影响干扰T。
理论证明:当我们拥有完美的RCT实验时,由于 t 跟 x 不再有关系,所以就没有了后门路径。
因果性证明:
问题阐述:证明“do 算子下的 y” 等于“ t 条件下的 y”,即证明因果就是相关。

证明得到:RCT数据中,相关性即因果性: Correlation does imply Causation
工业界现实情况
1.协变量往往会造成研究结论的偏倚。
实际工作中若仅用简单随机化,则很难保证有些重要的协变量的平衡,尤其是当试验的样本含量较小时,随机对照研究也会出现分组不均衡的情况。如果出现协变量不平衡,而它们又与研究结果密切相关时,则这时不合理考虑协变量的影响,直接评价处理效应, 将很可能会导致结论的偏倚乃至错误,此时的协变量便是混杂因素,带来混杂偏置。
2. 工业界中我们研究的是对特定场景或者人群的因果效应,即我们的应用更多是从ATE变为了CATE 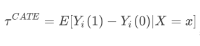
,即对确定性的特征集合X下的因果效应,那么,对于Condition on X,我们如何具体检验是否均衡,以及不均衡是如何影响因果效应的?此时必须引入Positivity。
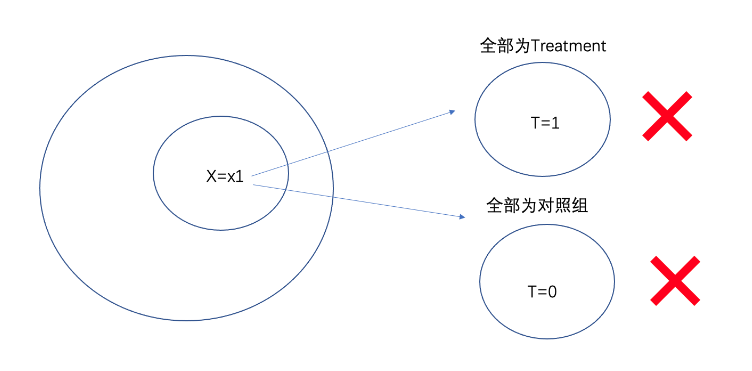
Positivity (common support)
对于任何的特征X,都不能对T有绝对性的影响。
即:要求treatment组和对照组的X有共同取值范围。
Positivity的重要意义:
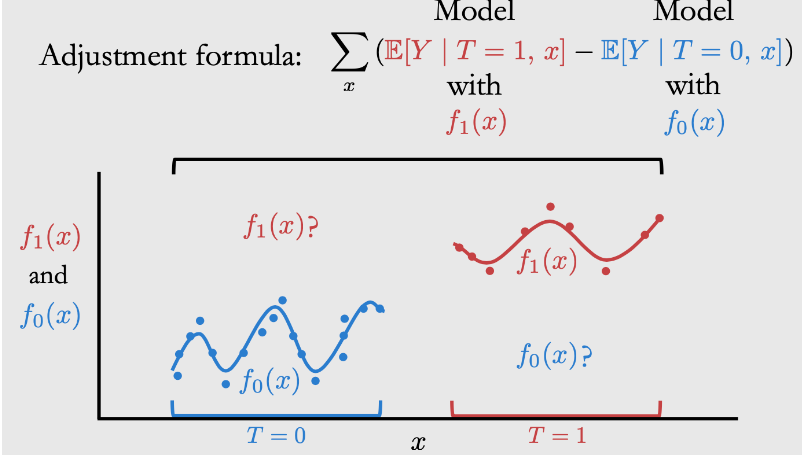
在下面这张图中我们用横轴表示x(covariate):
控制组不做任何干预T=0,输入x到输出Y符合f0分布,我们用f0这个模型来拟合表达,即蓝线。
试验组进行某个干预T=1,输入x到输出Y符合f1分布,我们用f1这个模型来拟合表达,即红线。
按照CATE公式,我们需要知道f1 在左侧蓝色区域的取值,以及f0在右侧红色区域的取值,然而由于不满足common support 我们在这些地方并没有数据,模型就会产生模型各自归纳的推断,不同模型选型或者处理方式就会带来归纳偏置,也将会导致结论的偏倚乃至错误。
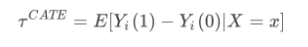
Positivity的痛点:
维度较多时能够满足Positivity的数据会越来越少。如下假设单一维度特征重合度为50%,那就只有50%的数据可以使用;如果是2维,那就只有25%的数据可以使用。算法的维度可能是几十甚至上百上千,想要满足Positivity,甚至互联网领域APP难度都极大。
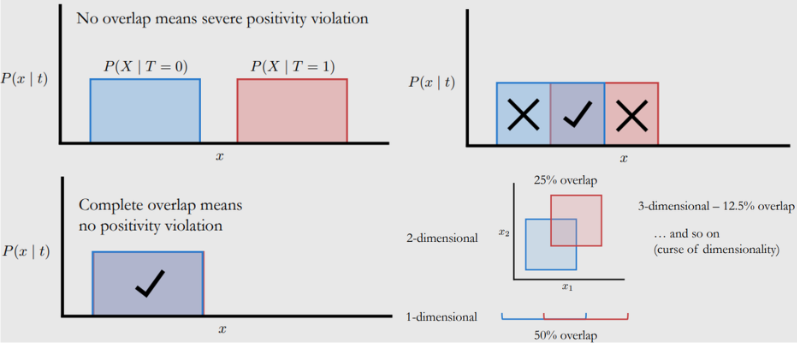
这个时候我们就会发现:Positivity和Unconfoundedness其实是一种tradeoff的关系
考虑了更多的特征covariates,一般而言无法做到positivity的要求
考虑了较少的特征covariates,一般而言无法做到Unconfoundedness的要求
无RCT数据因果求解方法
无RCT原因
Ethical reason: 随机分组要求实验组的人都抽烟,都吸毒
infeasibility: 随机分国家,要求实验组国家GDP降低,或者改变体制
Impossible: 随机分组,要求实验组的人员修改体内DNA
理论来看,无RCT数据的求解方法,就是通过一定方法手段使得数据满足RCT数据约束,制造虚拟的treatment组和control组。
这里将会简单介绍业内比较常见的方法和思路,并且在后续的工业界应用都可以看到相应的例子,我们依然从理论CATE公式出发,对如下5个方法做了归类:
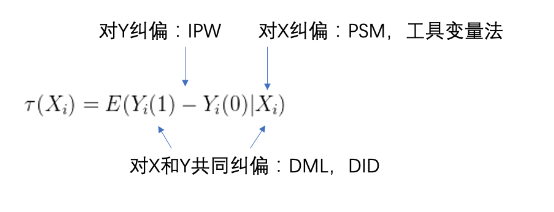
对X纠偏:PSM ,工具变量法
对Y纠偏:IPW
对X,Y同时纠偏:DML,DID
倾向性得分(Propensity Score)
假设当前我们已经做了相关Treatment,control组的实验,但是实验组和对照组的协变量分布不均匀。
倾向性得分是指:分布不均情况下即每个个体进入实验组的概率(多大可能性take treatment)
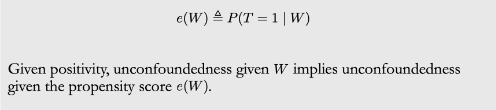
| 示例:在“睡觉穿鞋”是否导致“起床头疼”这个案例中,我们设定干预组T=”睡觉穿鞋“,对照组T=”睡觉不穿鞋“, 此时我们只有一个特征X=”喝酒“,进入不同组的概率就是倾向性的分e,如果P(T=”睡觉穿鞋“ | X=”喝酒”)=P(T=”睡觉不穿鞋“ | X=”喝酒”)=50%,那么我们就认为协变量分布均匀。 |
倾向性的分的出现解决的核心问题是特征维度过高带来的positivity违反。因为W维数过高,很可能会有positivity假设的违反,但是Propensity Score Theorem告诉我们,其实我们不需要以W为条件,我们只需要以这个一维的 e(W) 为条件即可。这么做positivity 违反的程度就大大降低了。
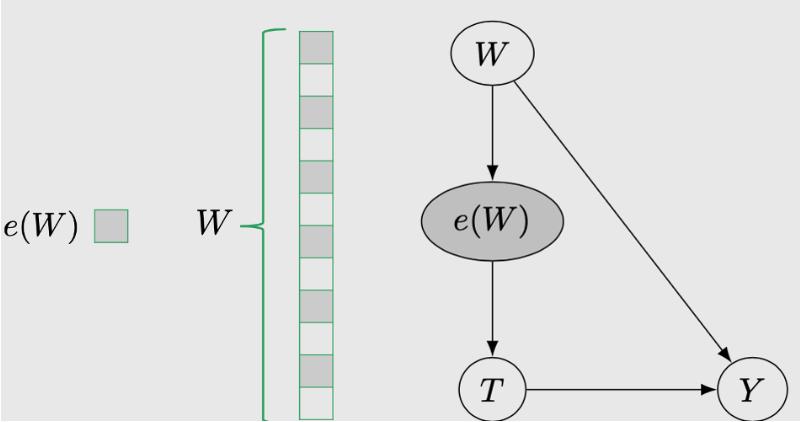
PSM(Propensity Score Matching)一般工业界用法:
1.选择同时影响treatment与outcome的特征,基于特征对treatment进行二分类建模,得到倾向分;
2.在支撑集上,基于重要特征与倾向分进行匹配,为被干预用户找到匹配的样本;
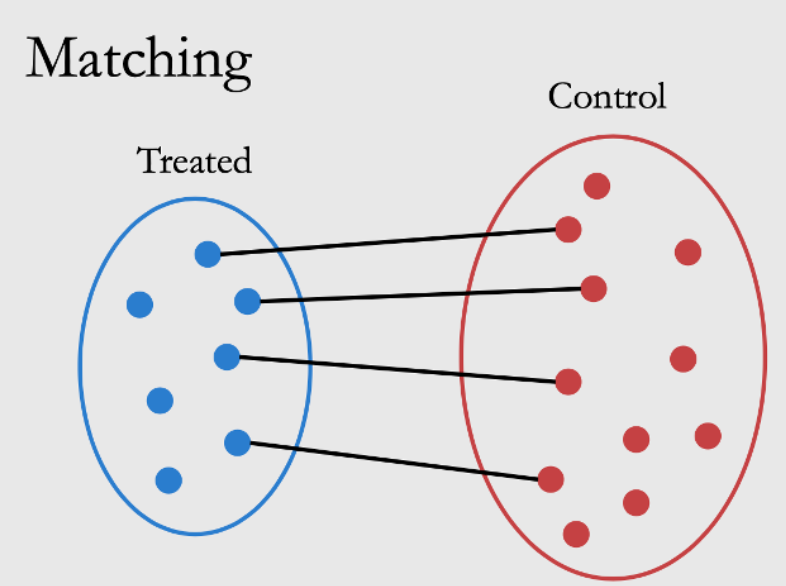
3.对匹配结果的质量进行检验,检验通过的话进入下一步,否则返回第二步进行匹配的优化;
4.增量计算。
PSM的问题:
PSM只控制了可测变量的影响,如果仍然存在不可测变量选择 ,仍然会带来隐形偏差。 PSM匹配只是对局部影响的评估,未能matching的样本,无法得到因果效应,即PSM的研究忽视了样本间的不平衡性。
工具变量
在我们谈到后门路径的时候,提到过因果的一个假设 没有未观测到的混淆变量 基于这个假设直接回避了隐藏的混淆因素(hidden confounders )带来的问题。但显而易见,这个假设往往很难完全满足的,既然我们关心的因变量(treatment)会受到隐藏的混淆因素影响,那么,是否可以找一个不受隐藏的混淆因素干扰的工具变量间接预估因果效应。
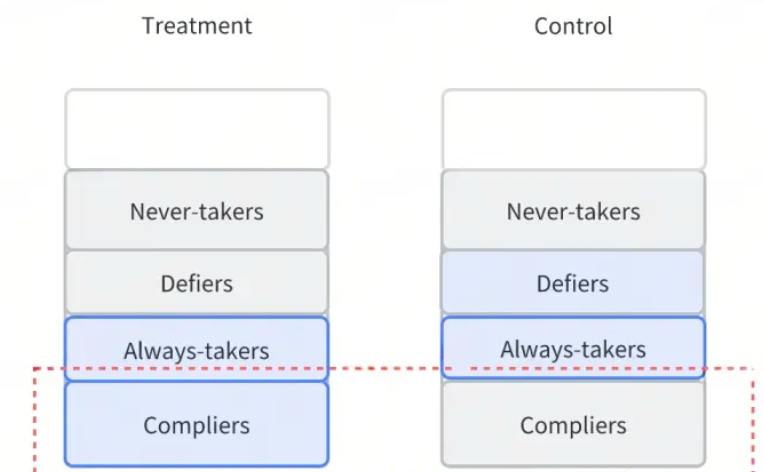
在随机实验中,随机选择一部分人在treatment组,另一部分在control组,但是根据施加的treatment和实际的treatment的不同,可以分为4类人:
- always takers:无论在treatment组还是在control组,都能够获得treatment
- never takers:无论在treatment组还是在control组,都不能够获得treatment
- compliers:在treatment组一定会获得treatment,在control组则一定不会获得treatment
- defiers:在treatment不会获得treatment,在control组则会获得treatment
比如给用户发红包的业务场景为例,在treatment组的用户会曝光红包,用户可以选择领取或者不领,因此领取的用户可以认为是compliers
比如新上线了某款产品的场景为例,在treatment组的用户会曝光产品,用户可以选择下载或者不下载,因此下载的用户可以认为是compliers

这里always takers和never takers没有因果性,不予以考虑;Defiers不符合单调性原则,不认为存在。因此我们住需要求解Compliers的因果性。

这里我们求的是局部的因果效应LATE(local average treatment effect)。
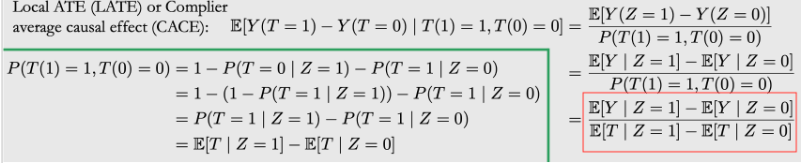
工具变量的约束:工具变量只能通过影响 treatment来影响 outcome Y;
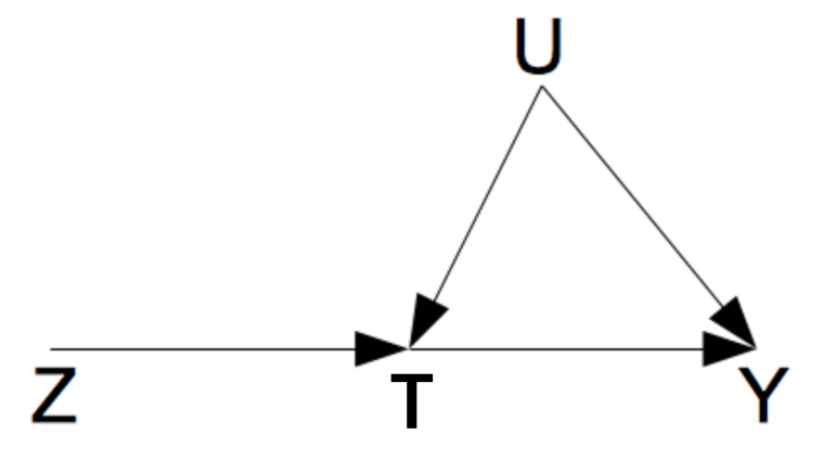
即现在找到了一个工具变量 Z ,这个工具变量Z与treatment T 相关,即
只能通过 影响 treatment T 来影响 outcome Y,与其他会影响到Y的因素无关,即
其中v为其他混杂变量
工具变量法的核心思想: 如果我们能通过对业务理解与统计模型构造出这样一个干预变量Z,那我们就可以对我们关心的群体因果效应值进行无偏估计。一方面我们需要深刻的业务理解找到适合的工具变量,另一方面我们也需要合理利用统计工具检验候选的工具变量是否满足条件。但第二点
 ,通常是无法确认的,只能争取或说服大家。怎么保证说工具变量Z 一定与 Y没有直接关系,Z 只能通过T 间接影响Y,即这是Z唯一影响Y的路径。
,通常是无法确认的,只能争取或说服大家。怎么保证说工具变量Z 一定与 Y没有直接关系,Z 只能通过T 间接影响Y,即这是Z唯一影响Y的路径。
另外工具变量只能探究工具变量特征下的局部的因果性,工具变量条件下的因果性求解方法可以通过2SLS,这里不做展开。
IPW
重加权即通过对Y进行干预,移去了由混杂因素到T节点的关系。如下,我们知道W和T相关,我们通过求取W对T的影响(这里一般就是求取倾向性得分),直接对结果Y进行加权,从而得到因果性。
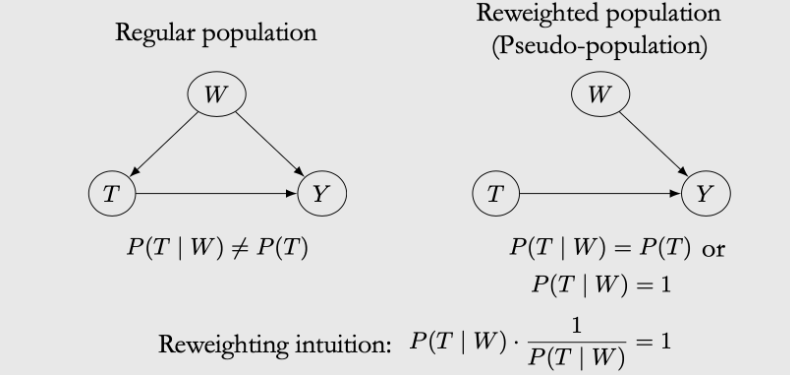
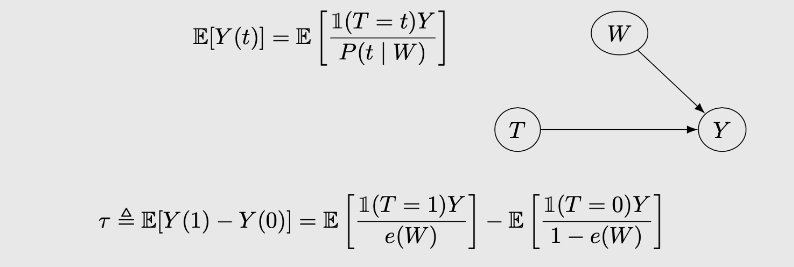
示例:
已知 干预组T=”睡觉穿鞋“,对照组T=”睡觉不穿鞋“,其中穿鞋睡觉第二天头疼的概率为90%,即
E[Y=“头疼”|(T=”睡觉穿鞋“) ]=90%,
E[Y=“头疼”|(T=”睡觉不穿鞋“) ]=10%,
假设不存在混杂因子“喝酒” ,那么ATE:
ATE=E[Y=“头疼”|(T=”睡觉穿鞋“) ]-E[Y=“头疼”|(T=”睡觉不穿鞋“) ]=90%-10%=80%,穿鞋大概率导致第二天头痛。
此时,我们只有一个特征X=”喝醉“,假设 喝醉后睡觉不穿鞋的概率是90%,即P(T=“睡觉穿鞋”|W=“喝醉”)=90%,那么通过IPW加权后:
ATE=[90%/90%]-[10%/(1-90%)] = 0,从而得到穿鞋不是第二天头痛的原因。
DML
第一步通过输入的特征去分别预测个体获得的treatment和产出的outcome。
第二步再去对于残差(residual)进行预测
T的残差可以看作将X对T的作用从T中去除后剩下的量,此时T的残差独立于X。而利用X对Y建模的作用在于去除Y中X的作用,即去掉了W–T和W–Y的路径,于是对残差建模只剩下T->Y的了。

示例:干预组T=”睡觉穿鞋“ 中有100人,其中90人喝酒,我们剔除这90个人; Y=“头疼”的人恰恰就是这个90个喝酒的人,我们也做剔除;最终我们发现实验组剩余的10个穿鞋的人和对照组的人都不头疼,即穿鞋不会导致头疼。
DID
存在一些场景完全无法找到对照,但是可以找到随着时间变化趋势一致的两个差异分组,用后面时间点的outcome减去前面时间点的outcome,我们可以扣除这种时间趋势的影响,而这时实验组和对照组的差距,便是treatment的作用了。(这里的treatment group直到某个唯一时间点才会得到它的treatment。)
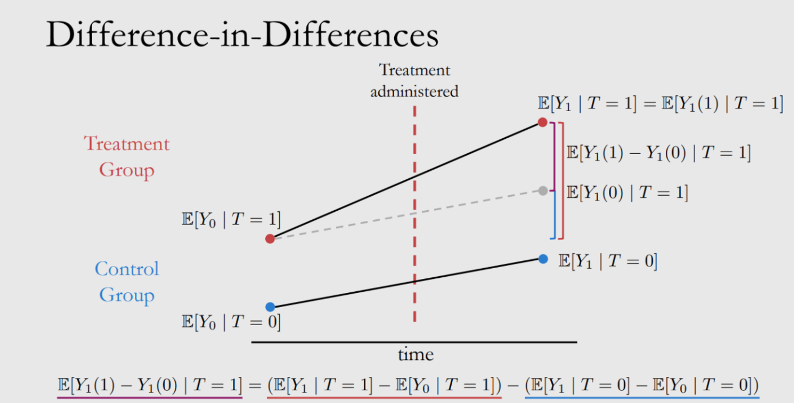
(1)可以很大程度上避免内生性问题的困扰,一定程度上也缓解了遗漏变量偏误问题。
(2)传统方法下评估政策效应,主要是通过设置一个政策发生与否的虚拟变量然后进行回归,相较而言,双重差分法的模型设置更加科学,能更加准确地估计出政策效应。
(3)双重差分法的原理和模型设置很简单,实践性较强。
因果预估方法
什么是Estimation?
工业界常常通过做过A/B实验得到因果性的价值评估,与此同时,我们希望通过历史的实验结论,沉淀为一套模型方法,帮助对于未来的判断。
比如,医学界通过双盲实验检验了某种药物的疗效,此时新来一位特征为{男性,年龄60+,有高血压}的用户,有经验知识的医生会告诉他服用该药成功率是80%。
比如,叮咚APP通过RCT实验,获得了实验组发放满39-10优惠券 VS 对照组不发放优惠券的GMV增量,现在运营想要知道我们该给哪些用户发放优惠券带来的增量效果更好呢?
这里就需要算法能够训练和学习实验得到的知识,形成模型,为模型输入对应的用户特征(协变量),得到对应的潜在结果。
一般的算法逻辑:Y=F{权重1特征1+权重2特征2+权重3*特征3…. },
这里特征是用户属性即模型输入;Y是模型输出;F是不同的框架,比如LR或者深度学习本质是函数(即复杂的数学公式);权重是算法不断的灌入实验的历史数据,从而让模型学习到不同特征对于结果影响权重。
训练阶段输入历史的用户X的特征和观测结果Y,迭代训练直至等号左右偏差最小。
训练好之后,我们将任何一个用户特征输入后,就能预估出结果Y。
Uplift框架下:
具有RCT条件下我们对因果定量的预估的一般方法: one model,two model,深度网络TarNet为基准的网络结构
比如算法的一般解法:
uplift = F{权重1W1+权重2W2+权重3W3….+权重T(=1)} - F{权重1W1+权重2W2+权重3W3….+权重T(=0)}
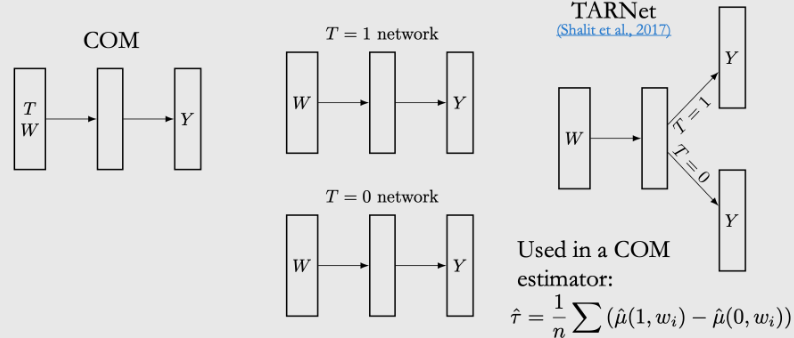
因果理论的不足
业界对Donald Rubin这套鲁宾因果框架存在一定的质疑,主要有以下几个方向
不是所有的因果都有先后顺序:爱打羽毛球 → 不断练习 → 羽毛球技术提升 → 爱打羽毛球 → 不断练习 → 羽毛球技术提升… 倾向性得分理论可以推导出因果性,但是倾向性得分不可获得:模型学习到倾向性分数具有主观性,不同模型和特征的倾向性分数不统一,没有明确标准。 不是所有混杂因子都是可被观测的:比如最早发现吸烟带来肺癌;后来发现尼古丁(混杂因子)导致肺癌,没有尼古丁吸烟也不会肺癌;再后来发现尼古丁和具有某个基因(混杂因子)的结合才能导致肺癌,没有该基因的人不会肺癌。显然随着科学技术和领域的不断进步,我们能观测到的内容会越来越多。而站在当下,我们假设所有混子因子我们都可被观测和考虑,显然是武断的。
因果效应评估方法应用案例
因果效应的评估方法包括两大类:
实验评估:通过大量随机对照实验(RCT)得出结论。因果推断的难点在于反事实,因此对照实验需要“足够随机”,对实验环境要求比较苛刻、成本相对较高且费时费力的。 观测性研究:对于已有的观测数据,通过建模进行因果关系的研究。该方式对数学的要求较高且存在准确率的问题,但可应用面和可操作性强,因为实际情况中往往无法直接进行随机实验,比如政策发布、病理研究等。
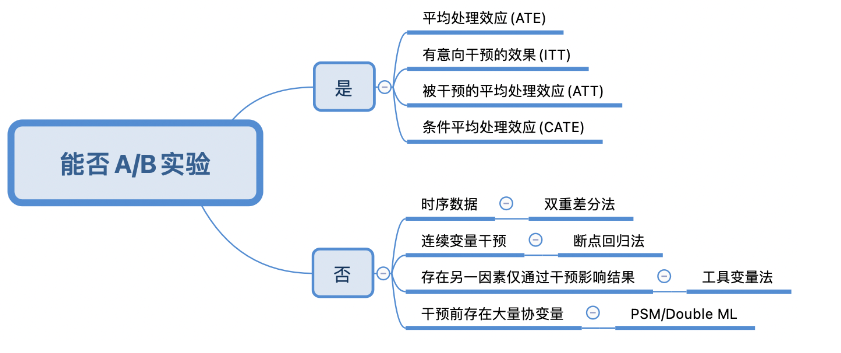
A/B实验RCT数据
评估方法:ATE,Average Treatment Effect,平均处理效应
两组用户随机分流,实验组(Treatment)的所有用户受到干预,对照组(Control)的所有用户未受到干预。
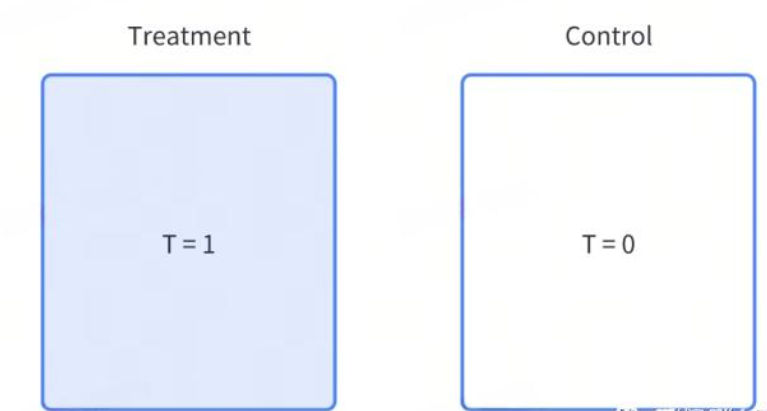
评估方法:ITT,intent-to-treat Effect,有意向干预的效果
有很多策略在实际中并不能对每一个用户生效,例如如果我们希望度量某一个广告的效果,理想情况下我们希望实验组的用户都看到这个广告,对照组的用户都看不到。但现实情况是,当你向实验组的所有用户投放广告后,大部分用户并不会打开app,因此也就无法看到广告。那么,实验组中就仅存在一部分用户实际看到了广告,他们就是实际被策略干预的用户,也就是图左边被标蓝色的部分。此时如果我们来统计实验组与对照组的差异,就称为ITT
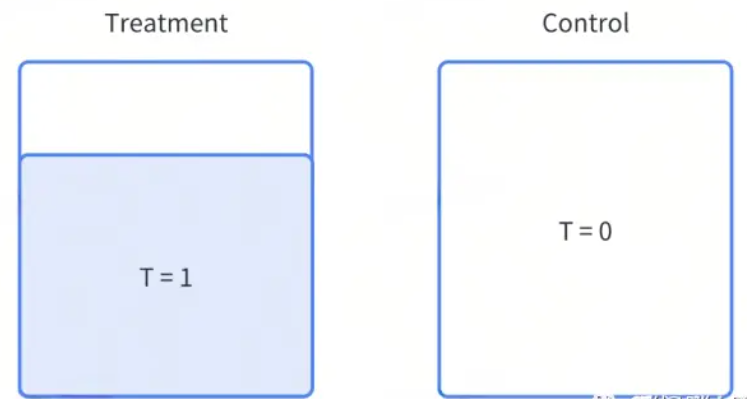
评估方法:ATT,Average Treatment on the Treated,被干预的平均处理效应
还是延续度量广告效果的例子,如果我们只挑选出实验组被广告曝光的这部分用户(图左边标蓝的部分),再找到与其完全同质对照组用户(上图右边标灰的部分),二者的差异就称为ATT
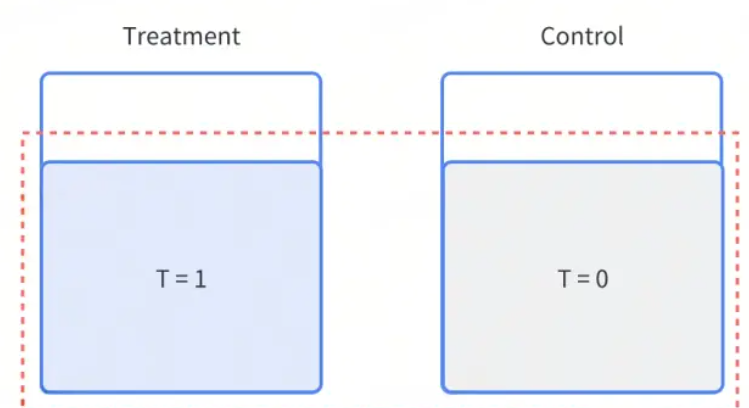
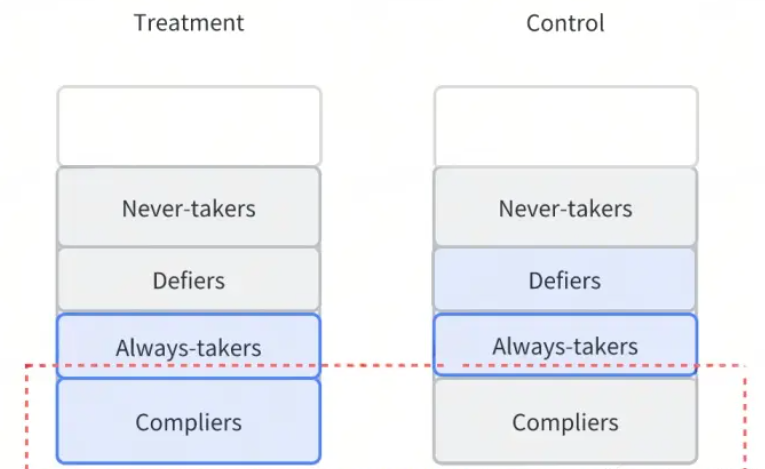
评估方法:LATE(CACE),Local Average Compliers Effect,条件平均处理效应
在理解LATE及与ATT的区别之前,我们需要先明确一下用户的区别:在实际的实验中,用户会分成以下几类:
Compliers:仅在被广告曝光后会发生转化 Always-takers:不论是否被广告被曝光,都会转化 Defiers:仅不被广告曝光会发生转化 Never-takers:不论是否被广告被曝光,都不会转化
LATE就是针对Compliers,即实际会被策略影响的用户,去度量策略的影响效果。ATT评估的是被treat的人的效果,被treat的人包括Always-takers+Compliers,LATE只评估compliers的效果,即图红框的部分。用公式表达为
非A/B实验非RCT数据
在无法进行A/B实验场景下,即观察性研究中进行因果推断的最核心在于通过对观察性数据的理解与分析,建立合理的干预&对照分配机制,即在给定干预变量 T 和协变量 X 的分布, 从原始数据里选取与构造虚拟的试验组与对照组, 满足:
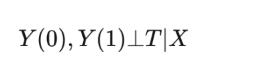
一般地,在观测数据的因果推断中,我们会优先看数据是否满足断点回归、双重差分法、工具变量的前提要求。如果满足,会优先使用这三种方法;如果不满足,才会使用倾向评分匹配法(Propensity Score Matching,PSM。这种优先级的原因是相比于PSM,前三种方法绕开了混杂因子,这是唯一的也是最重要的区别。因此它们依赖的假设在业务层面更容易得到满足,同时也很容易被检验。
断点回归法
2.1.1 原理
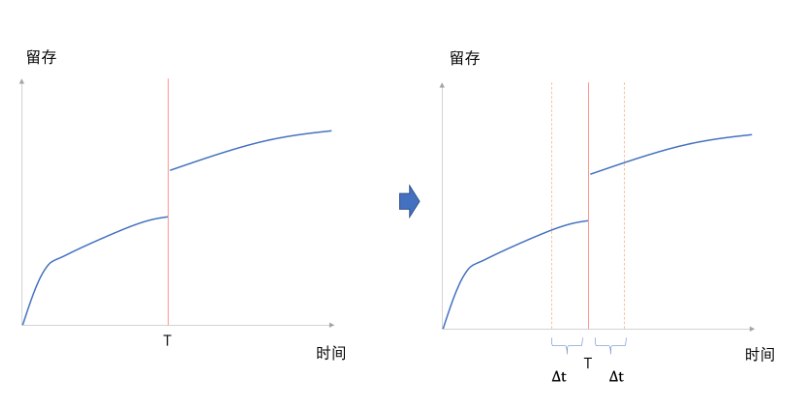
断点回归利用一个预先设定的”断点”或”临界值”,在这个断点两侧的个体间比较结果变量,以此推断因果关系。断点回归的关键在于它假设在断点的紧邻区域内,个体是非常相似的,即紧临区域内混淆因子效用一致,从而构造虚拟的试验组与对照组,排除干扰。例如,研究上大学对于未来财富的影响,考试分数恰好在录取线上下的学生,在其他许多特征上(智力)可能相差无几。因此,任何在断点两侧观察到的结果变化,都可以归因于是否接受了大学教育的干预,而不是其他因素。
2.1.2 适用场景
确定短期指标和目标,或者确定干预时间点。 例如,T时刻是否为转化关键时间点。 我们首先确定时间T,认定使用T时间以上的用户为treatment组,T时间以下的用户为control组,如果前后个体非常相似,那么T时刻就是AHA时刻。
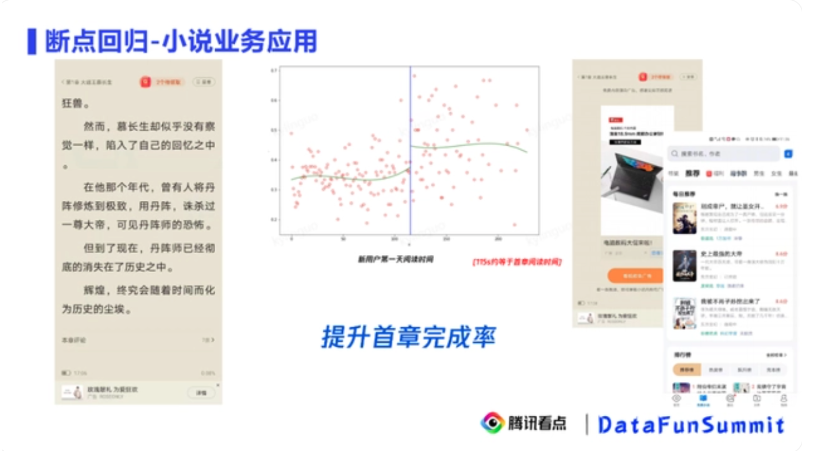
2.1.3 业界案例:腾讯小说业务场景
案例诉求:研究新用户第一天的阅读时间对次日留存的影响(https://baijiahao.baidu.com/s?id=1718536872920523609&wfr=spider&for=pc)
结论:提升新用户的首章完成率可以提升新用户的次留
逻辑:
如图,横轴是新用户第一天的阅读时间,纵轴是新用户的次留。我们发现新用户第一天的阅读时间和次留间存在明显的端点,大概在115s左右。这个时间大约是阅读完一章的时间。因为是新用户,恰好是新用户的首章阅读时间。因此我们发现提升新用户的首章完成率对新用户的次留有因果效应。为什么说这是因果效应呢?因为115s左右是一个连续的邻域,我们可以认为其在邻域中各种混淆变量基本不会有太大的差异。根据这个结论,我们应该以提升新用户的首章完成率作为目标。针对这个目标,我们有如下建议:
在首页推荐时,以小说易读率作为一个指标,不优先考虑进入节奏比较慢的小说
取消首章阅读的广告,来提升首章完成率,从而提升用户的次留
类似案例:
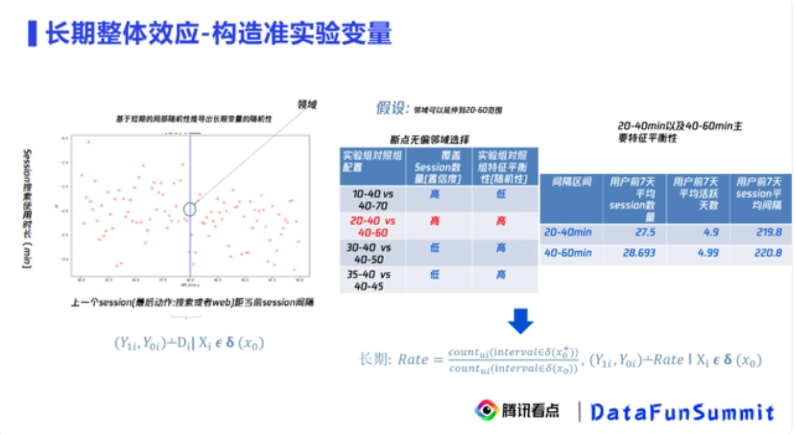
工具变量法
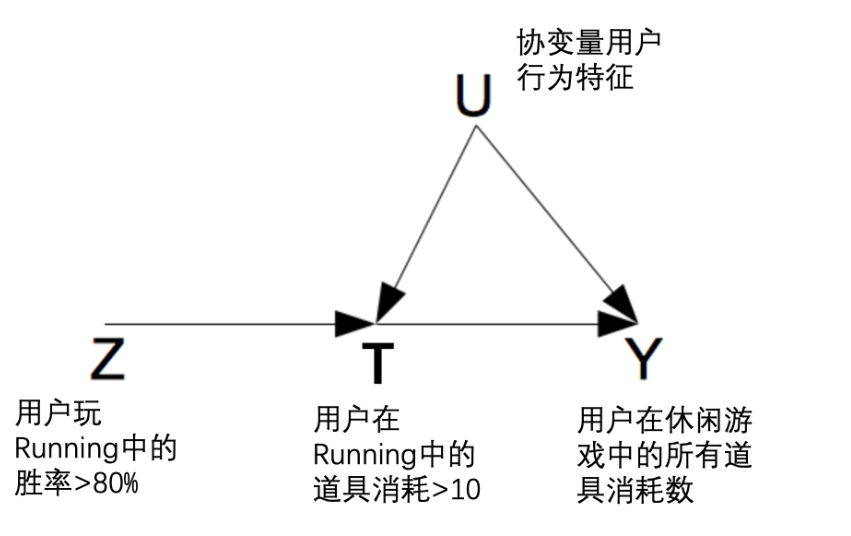
2.1.4 业界案例研究:Bigo Live公司上线一款游戏Running-Bigo对整体休闲类游戏营收效果是否正向。
(https://mp.weixin.qq.com/s/PFFltyXQSEWokd-EPJuMWA?poc_token=HMOW1WWjwlC6u2vy0N3kI7JY0jg1jMnUMpA_DLys)
案例背景:Running-Bigo是Bigo Live在2020年自研的一款休闲类游戏。在产品上线后的一个多月, 针对Running用户增长的数据,业务部门的领导们提出了如下问题:
用户在Running里花费较长的时间,会挤压其他游戏的时长投入和营收吗?
针对整个休闲游戏体系,我们引入Running-Bigo对整体的用户营收效果与平台生态又该如何评估呢?
直接基于观测数据,比较玩Running和不玩Running的人的人均营收对比,显然存在很大问题,两者人群不同质,不是RCT数据无法得到因果性。
Bigo Live给出的解决方案:
目标定义:研究如何量化用户在Running的道具消耗对用户在整体休闲类游戏道具消耗的影响的因果效应值。
在该案例中,工具变量法的框架整体定义如下:
定义treatment和control的标准,即干预T :用户在Running中的道具消耗数 (取对数); 即,假设用户在Running中的消耗大于某个值为treatment组,否则为control组。
Z工具变量 :用户玩Running时的胜率;
Y目标值 : 用户在休闲游戏中的所有道具消耗数 (取对数);
U协变量 :主要包括用户在Running上线前后的道具消耗数的各种统计数值 (取对数)和其他一些业务相关的特征变量;
为什么工具变量是:用户玩Running时的胜率? 原文的解释是:
“这里有一个业务上的理解与假设,为什么在Running中用户的胜率可以当作工具变量? 一个前提:Running是当前Bigo Live休闲集合中策略性最强的,即运气成分比较弱的。用户可以通过自己的游戏水平决定自己的游戏参与情况(还有其他因素考量,由于业务原因这里不便展开)。”
之后,进行一定的检验并通过2SLS方法得到ATE置信正向,也就是表示用户在Running消耗道具对整体休闲游戏的道具消耗是有正向作用的。
思路解读:如下假设离散情况下,胜率大于80%的人,才能受到Running上线的影响,所以我们只需要研究这部人。而胜率与用户道具的消耗相关,即现在找到了一个工具变量 Z ,这个工具变量Z与treatment T 相关,并且只能通过影响 treatment来影响 用户在休闲游戏中整体的道具消耗;最终求解得到因果效应。